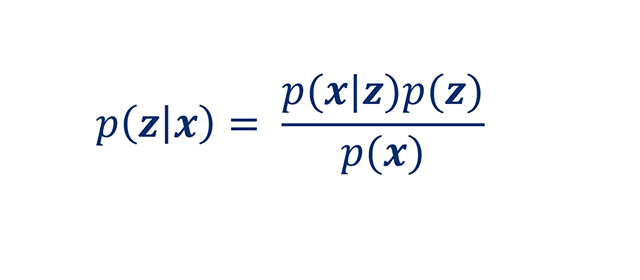机器学习:贝叶斯推理

中使用的计算机视觉的计算,贝叶斯推理是一种更新模型假设的方法z以下是对数据的观察x．

它利用了贝叶斯定理

关于潜在变量的先验假设z, p (z),在新一批数据之前量化我们的信念x是观察到的。我们假设数据x都是在不断的数据生成过程中产生的，p (x)我们可以量化观察的可能性x鉴于我们的假设z通过条件分布p (x | z)．尽管贝叶斯推理是一个有点抽象的概念，但它在现实世界中有很多应用，是支持许多机器学习技术的强大工具。一个非详尽的应用程序列表包括:

• 概率和生成建模-例如图像标准化和变分自动编码器
• 参数模型的不确定性量化——例如贝叶斯神经网络

贝叶斯推理最普遍的应用之一是不确定性量化。例如，在参数回归中，我们观察到的数据实际上是一对数据(x, y)我们的任务是预测标签y在新的数据点上x，因为我们得到了后验分布的封闭表达式p (z | {x, y})．注意，在这种情况下，可能性有固定形式的p (y | x, z)．然后用后验预测分布量化不确定性，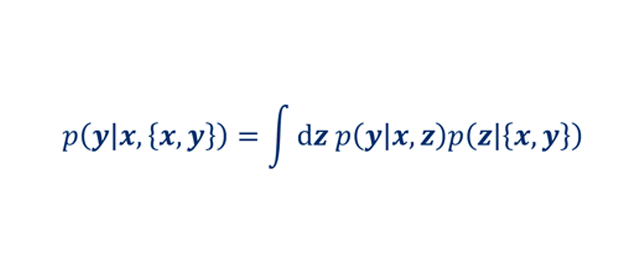

Which在有限的情况下具有封闭形式的表达式，例如whenp (y | x, z)正态分布是否具有各向同性的标准差，其期望值是的线性模型z．否则，样本的潜变量z一定是从后验分布产生的吗p (z | {x, y})的期望值和方差p (y│x, {x, y})必须用数字来计算。

值得对贝叶斯推理的介绍做一个总结的是，这里所描述的贝叶斯定理的应用假设我们有一个计算后验分布的封闭表达式p (z│x)．这并不总是情况和近似p (z│x)必须经常作出，以便使用模型预测，例如通过后验预测分布。机器学习的一个大分支叫做近似推理，实际上就是为了实现这一点而存在的。

在Element，我们在数字工程操作中使用贝叶斯推理方法。联系我们的数字工程团队为更多的信息。